 |
> Достоверность расчетных длин в RFEM | |
Достоверность расчетных длин в RFEM |
||

|
|
||
| | Правила | Регистрация | Пользователи | Сообщения за день | | Поиск | | Справка по форуму | Файлообменник | |
|
|||||||
 |
| Поиск в этой теме |
|
||||
|
REконструктор истины Регистрация: 23.02.2006
M...nsk
Сообщений: 184
|
Цитата:
 Систематизируем все хоть как-то. 1. Есть основная программа RFEM, в которой определяются усилия и деформации. 1.1. Какие в ней назначены мю - на результаты в основной программе никак не влияет. 1.2. Результаты при линейном и нелинейном анализе будут разные. 2. Полученные результаты передаются в модуль расчета по формулам СП (или еврокода - неважно). 2.1. Участники форума утверждают, что коэффициент мю при нелинейном расчете стержням назначать не имеет смысла. 2.2. Участники форума утверждают, что результаты расчетов на устойчивость при нелинейном расчете (в основной программе) можно игнорировать. При условии правильного задания нагрузок типа "Несовершенство". Мне теоретические дебаты интересны в последнюю очередь. Меня интересует практическое правильное использование конкретного инструмента. Поэтому несколько пояснений как я его использую. 1. Метод решения всегда нелинейный. 2. Отказ от использования стержней типа "Сжатие". В основном используются "Балка", "Растяжение", "Канат". Соответственно, любой расчет на потерю устойчивости - это расчет на устойчивость "изгиба и сжатия", "изгиба и сдвига", "изгиба и поперечной силы". Расчета на потерю устойчивости "сжатие" в моих моделях практически нет. 3. Использовать нагрузку "Несовершенство" я не планирую. Как довесок к основным нагрузкам она мне мало интересна, а плодить сочетания нагрузок в геометрической прогрессии не хочу. 4. Потеря устойчивости - основной критерий для большинства моделей. Ввод (или не ввод) "правильного" мю прямо (и сильно) влияет на результат. 5. Резюме модуля расчета по формулам - путевка в жизнь для каждого стержня. Игнорировать его результаты на основании тезиса "Программа - дура, пользователь - орел!" не хотелось бы. Вопросы. 1. Если отказаться от нагрузок "Несовершенство", то гарантированно правильных расчетов по формулам при условии, что мю=1 мы не получим в любом случае? 2. Если по усилиям из нелинейного расчета мы делаем расчеты по формулам, используя "правильные" (для линейного расчета) мю, то всегда получаем завышенные значения расчетных сочетаний? 3. В расчете по нормативной методике на устойчивость сжато-изгибаемых стержней действительно можно игнорировать мю, при условии нелинейного расчета с нагрузкой "Несовершенство"? Добавочные усилия на деформированном стержне делают его эквивалентным эйлеровскому шарнирно-опертому с мю=1?
__________________
YouTube Последний раз редактировалось tentovic, 22.02.2023 в 14:18. |
|||
|
|
|
||||
|
Инженер-философ Регистрация: 24.04.2019
Хабаровск
Сообщений: 2,083
|
По-моему, их первое возражение повторяет мою версию появления коэффициента 1.3 в нормах: Методы определения расчетных длин пригодных для расчетов на устойчивость по СП 16.13330. Ищем, делимся, обсуждаем. Пост #226
Другими словами: в конструкциях малой гибкости нелинейный расчет дает достаточный запас до разрушения, а в гибких он сходится к Эйлеру и к критической нагрузке. То есть ни искривления, ни свойства материала в гибких схемах уже не влияют на запас, и без дополнительного коэффициента геомнелин назначает несущую способность вплотную к критической. Поэтому приходится считать и нелин, и устойчивость, а потом выбирать минимум. Цитата:
Нормативная методика расчета даже шарнирного стержня с мю, заведомо равным единице, состоит из:
И чем любая рама хуже простого стержня? Не говоря уже о том, что она по сравнению с одиночным стержнем добавляет дополнительных сложностей. |
|||
|
|
|
||||
|
REконструктор истины Регистрация: 23.02.2006
M...nsk
Сообщений: 184
|
Цитата:
 Всегда считал, что надо назначать мю каждому стержню и считать устойчивость для каждого стержня в модели. Но убеждают, что при нелинейном расчете это принципиально неверно. Надо признать - результаты линейного и нелинейного на примитивном примере с консольной стоечкой действительно отличаются. Вылет за границы применяемости линейного? Вроде нет. Выполняем по всем правилам линейный расчет с мю=2, имеем расчетное сочетание по устойчивости - 0,99, вертикальная сила - 50 кН. Считаю СН с несовершенством из IMP'а и нелинейным расчетом, сходится при вертикальной силе уже 40 кН. Критическая сила - 63,81 кН. По логике - 50/63,81=0,78<1.
__________________
YouTube Последний раз редактировалось tentovic, 23.02.2023 в 17:08. |
|||
|
|
|
||||
|
REконструктор истины Регистрация: 23.02.2006
M...nsk
Сообщений: 184
|
Что касается рам, просчитал вот такую халабуду под нагрузками от балды. Мюшки стоек >1 только в плоскости рамы.
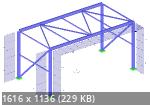 Линейный, мю=4 (теоретическое - 2) 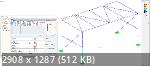 Пидельта, мю=4 (теоретическое - 2)  РБП, мю=4 (теоретическое - 2)  Пидельта, мю=1  РБП, мю1  1. Разница линейный/нелинейный не велика. 2. Разницы на мю=1 и мю=4 в нелинейных вообще не обнаружено, вклад от продольной силы переоценивать не стоит. 3. На расчете РБП ригель вынесло кручением.
__________________
YouTube Последний раз редактировалось tentovic, 22.02.2023 в 20:22. |
|||
|
|
|
||||
|
REконструктор истины Регистрация: 23.02.2006
M...nsk
Сообщений: 184
|
Теперь рассмотрим пару сквозных арок.
Нагрузки условные: слева - давление, справа - отсос, в пояс одной из арок - давление. Мю поменял на правильные только на 4-х пролетах влево и на 4-х пролетах вправо от коньковой дуги одной из арок.  Линейный с правильными мю  РБП с правильными мю  РБП с мю=1  У линейного и РБП с правильными мю - практически идеальное совпадение. У РБП с мю=1 - абсолютный бред. У РБП снова хронические проблемы с кручением. Стержни, выбитые кручением, модуль (как и на рамах постом выше) не отрисовывает. У пидельты таких проблем с кручением либо меньше, либо нет вовсе. Вот и все, что требовалось доказать! ----- добавлено через ~14 мин. ----- Цитата:
Инженеры уверено двигаются в этом направлении. И это прекрасно! Пускай разработчики ПО мозги сушат. (Шучу, если что!)
__________________
YouTube Последний раз редактировалось tentovic, 23.02.2023 в 12:53. |
|||
|
|
|
||||
|
КМ (+КМД), КЖ (КЖФ) Регистрация: 30.05.2007
Далече
Сообщений: 25,652
|
Цитата:
 Цитата:
Что именно Вы там доказали таки?  Можно повторить два раза и помедленней для нешумахеров? Можно повторить два раза и помедленней для нешумахеров? |
|||
|
|
|
||||
|
REконструктор истины Регистрация: 23.02.2006
M...nsk
Сообщений: 184
|
Цитата:
 А все остальное - фантазии, которые к делу не пришьешь. *** Что касается "Момента-устойчивого-равновесия-ферштейн" и волшебной палочки "Несовершенства". 1. Да, при нелинейном расчете сам расчет слетает, если модель неустойчива. И разработчики RFEM посылают прямиком в модуль STABILITY. 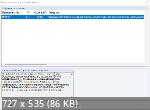 "Матрица жесткости сингулярная! Модель неустойчива. Обнаружена потеря устойчивости в узле сетки КЗ № 8, направление phi_X, приращение 1 .Заданная нагрузка превышает критическую нагрузку. Можно рассчитать коэффициенты критических нагрузок и потери устойчивости в дополнительном модуле RF-STABILITY при помощи метода увеличения нагрузки до точки разрушения конструкции". Факта завершенного расчета мало  для того, чтобы ограничиться анализом эквивалентных напряжений в RF-STEEL-MEMBERS. Соблюдение норм предполагает учет тех же коэффициентов безопасности, к примеру. для того, чтобы ограничиться анализом эквивалентных напряжений в RF-STEEL-MEMBERS. Соблюдение норм предполагает учет тех же коэффициентов безопасности, к примеру.2. Несовершенства могут казаться волшебной палочкой из-за того же отклонения от прямолинейности. Но это не так. Несовершенства можно (и нужно) рассматривать как просто еще один вид нагрузки. В своих моделях, где стержни преимущественно типа "Балка" и имеют собственный вес, с трудом могу представить где, под нагрузкой, стержни могут остаться прямолинейными, плюс сам метод больших перемещений предполагает деформированную схему. Нужны ли мне несовершенства в принципе? - См. еврокод: (7) В соответствии с (3) устойчивость отдельных элементов должна быть проверена следующим образом: а) если эффекты второго рода в отдельных элементах и соответствующие несовершенства элемента (см. 5.3.4) полностью учитываются при статическом расчете конструкции, то проверка устойчивости отдельных элементов согласно 6.3 не требуется; 5.3.4 Несовершенства элемента (1) Местные изгибные отклонения элементов учтены в формулах определения несущей способности элементов по устойчивости, см. 6.3. Отсюда выводы: 1. В еврокоде эксплицитно  описываются два способа расчета: описываются два способа расчета:- линейный, в одном из своих вариантов - с мю и расчетными длинами; - нелинейный с несовершенствами. Но имплицитно  не запрещено использовать нелинейный с расчетными длинами не запрещено использовать нелинейный с расчетными длинами  Поясню причину упорных выкрутасов с мю. Я не могу использовать линейный метод - он в программе недоступен из-за мембран. А несовершенства в нелинейном использовать не хочу. Ну представьте 3500 сочетаний нагрузок (СН). Именно столько получается при подвижной крановой нагрузке по методике из длюбаловского вебинара. Аддитивный принцип суперпозиции  не распространяется на результаты, рассчитанные по теории второго порядка (это о РС - расчетных сочетаниях). Каждый СН выбрать, решить, сформировать новое сочетание... Да и без крана СН дофигища обычно. не распространяется на результаты, рассчитанные по теории второго порядка (это о РС - расчетных сочетаниях). Каждый СН выбрать, решить, сформировать новое сочетание... Да и без крана СН дофигища обычно. 2. Если я выполняю расчет в модуле ЕС или SP (?) с формулами проверки устойчивости, то несовершенства мне нужны как собаке 5-я нога. Но тогда я обязан задать правильные мю при нелинейном расчете (с гипотетической вероятностью уйти в плюс по надежности). 3. Можно применить несовершенства как дополнительную нагрузку и в расчетном модуле отключить проверку на устойчивость. Как это грамотно сделать на практике? - Сделать отдельный расчет по каждому сочетанию нагрузок в модуле IMP, т.е. получить множество загружений типа "Несовершенство". Потом все их скрестить с уже имеющимися сочетаниями нагрузок. Таким образом, несовершенства, как лекарство от проверки устойчивости, при большом количестве сочетаний нагрузок на большой модели может оказаться хуже болезни. Кроме того, методика создания несовершенств в IMP вызывает сомнения в их соответствии значениям деформаций из норм еврокода (здесь могу ошибаться и тянуть на Dlubal напрасно). Одним словом - "Лекарство хуже болезни". Может и попробую на чем-то простеньком. *** И это правильно! Дай вам возможность управлять... Страшно подумать!  *** С праздником!
__________________
YouTube Последний раз редактировалось tentovic, 23.02.2023 в 18:07. |
|||
|
|
|
||||
|
REконструктор истины Регистрация: 23.02.2006
M...nsk
Сообщений: 184
|
Ильнур, спасибо!
 Вот, внял посылу ingt и почитал еврокод  Осознал свои ошибки, почти раскаялся. Перспективы альтернативы, конечно, неотрадные. Будем пробовать несовершенства, решать - стоит ли грешить с мю дальше  *** Если рассматривать нелинейные с мю не с тчк зрения де-юре, а с тчк зрения де-факто. На примере с арками мы не видим значимого расхождения в расчетных соотношениях при использовании мю и в линейном и в нелинейном расчетах. Значит, вклад доп. сил в нелинейном ничтожен (в данной конкретной модели). Рассмотрим расчет простейшей модели - стойка со свободным концом, 3 м, сечение ГСП 80х4, нагрузка - 40 кН, методы - линейный/пидельта, расчет по формулам еврокода. Линейный расчет с мю 2, расчетное соотношение (устойчивость) - 0,79. Нелинейный расчет с несовершенством - расчет состоялся (40 кН - на реальном пределе). Нелинейный расчет с мю 2, расчетное соотношение (устойчивость) - 0,79 (только продольная сила же). В варианте пидельта с несовершенством, 40 кН - предел. На линейном и на нелинейном с мю=2 можем подняться до 50 кН (расчетное соотношение на устойчивость - 0,99/1.01). *** Тот же пример, но выставляем вертикальную силу 40 кН и добавляем горизонтальную 0,1 кН. Линейный расчет с мю 2, расчетное соотношение (устойчивость) - 0,83. Нелинейный расчет с мю 2, расчетное соотношение (устойчивость) - 0,9. Влияние поперечной силы налицо. Вывод о возможном (!) излишнем запасе надежности по устойчивости в нелинейном расчете с мю=2, в сравнении с линейным, верен (на пределе р/с=1 мы будем вынуждены выбрать сечение больших размеров).
__________________
YouTube Последний раз редактировалось tentovic, 24.02.2023 в 00:57. |
|||
|
|
|
||||
|
Инженер-философ Регистрация: 24.04.2019
Хабаровск
Сообщений: 2,083
|
Цитата:
Линейный расчет получает N, равную нагрузке, и нулевые моменты. Это соответствует несущей способности RA (или RcrA), если искать Мизеса на изополях; разумеется, это неверно. Но, если сделать проверку по СП, через правильное мю программа найдет правильное φ, что физически будет соответствовать дополнительной проверке устойчивости и геомнелину, просто они будут сделаны по формулам из СП, а не прямо в МКЭ. Если несовершенство задано по нормам, а не от балды (буквально правильной формы и с точностью до сотых - тысячных миллиметра), то для конструкций малых и средних гибкостей расчет полностью совпадет с нормативным. Увидеть ответ можно по Мизесу, и проверку по СП делать уже не надо. И сила, и появившийся в расчете момент в сумме дадут пиковые напряжения, равные R - это и есть критерий прочности. Для гибких конструкций расчет завысит несущую. И он в любом случае должен получать ответ не более, чем расчет на устойчивость; если получилось наоборот, как в посте 126, значит, в расчете накосячено. Например, неправильно настроен решатель; видел такое в Скаде и в Старке. Или пропущена нужная форма потери устойчивости при задании несовершенства. Бессмысленное действие, потому что пытается дважды учесть одно и то же. Хотя в примере с консолью случайно дает правильный ответ, потому что без поперечных сил и искривлений "умный нелин" просто повторяет "тупой лин" или "тупую устойчивость", смотря как решатель устроен. В Старке, например, при разных галочках может находится как "лин", так и "устойчивость". Можно будет сделать, когда совпадут тестовые результаты расчета в программе, и ручной счет. Проверять надо версии малых, средних и больших гибкостей; с несовершенством и без; с поперечной нагрузкой в случаях малых, средних и больших эксцентриситетов; разных типов сечений. Все это надо сделать во всех возможных сочетаниях. В СП все эти "мелочи" переключают ход расчета и меняют результаты. И это только для начала, для консольного стержня. Потом уже можно ковырять дополнительные сложности в рамах. |
|||
|
|
|
|||||||
|
REконструктор истины Регистрация: 23.02.2006
M...nsk
Сообщений: 184
|
Цитата:
Если нижний пример (из моего предыдущего поста) посчитать в СП (где формулка оч. упрощенная, N), то разницы линейного с неинейным вообще не будет: Линейный расчет с мю 2, расчетное соотношение (устойчивость): EC - 0,83; SP - 0,91. Нелинейный расчет с мю 2, расчетное соотношение (устойчивость) - EC - 0,9; SP - 0,91. Цитата:
Цитата:
   Несовершенство же "нужно" только для нелинейного расчета. Ну как нужно? - Только формально нужно. И без него считает, если не циклиться на дотошных попытках вульгарно-натуралистично скопировать реальность в малейших деталях, а потом... умножить осн. нагрузку в 1,5 раза. А мало ли где накосячили?  Цитата:
Факт такой (см. пост 149): нелинейный расчет с несовершенством оказывается аутсайдером по максимальному значению вертикальной силы. Цитата:
Теперь о главном - почему это действие не представляется мне бессмысленным. 1. Нелинейный расчет с зашитыми мю прогоняется один раз (в идеале). На выходе из модуля расчета по EC/SP получаем удобные таблицы, где все удобно структурированно по расчетным параметрам, видно - где пусто, а где слишком густо. Есть возможность оптимизации сечений, наконец. Не срослось - меняем сечения, просчитываем еще раз. Из головной боли - назначить правдоподобные мю. 2. Нелинейный расчет с несовершенствами. Формируем сочетания нагрузок, которых будет очень много. Просеивать сочетания по параметрам - нет большого смысла, это тоже трата времени. По каждому сочетанию вводим данные в модуле STABILITY, решаем. По каждому сочетанию вводим данные в модуле IMP, решаем. Дублируем все сочетания, добавляем в новые СН соответствующие им загружения "Несовершенство" (сформированнные IMP). Запускаем - не срослось. Идем в модуль STABILITY, находим на каком стержне вылетело. Меняем сечение, считаем, ок - решение не слетает. В STABILITY сортировки нет, сквозная таблица по всем стержням. Придется тыкать в интересующие стержни на экране и прикидывать по критической нагрузке - где у нас густо, где пусто, как оптимизировать конструкцию. После этого - велкам на очередной круг.  И все это ради никому не нужного формализма и несовершенств, абсолютно не интересных и ненужных!!! Цитата:
1. Нелинейные с мю всегда будут давать запас по устойчивости по отношению к традиционному линейному расчету. На моих моделях этот запас будет от мизерно-отсутствующего (почти всегда) до приемлемо-незначительного. 2. Нелинейные расчеты с несовершенствами полностью коррелировать с линейными не будут. Какой бы тогда смысл в нелинейных с несовершенствами? Нелинейные, вероятно, все же будут давать менее оптимистичный результат (но более точный), чем линейные. И все это несовершенство методов (линейного гл. образом) расчета (в числе всего прочего) покрывается коэф. надежности (прежде всего - по нагрузкам). Чтобы проверить и так очевидное (абзацем выше) считаем тот же стержень, но с продольным усилием 1 кН и поперечным - 1,8 кН (уменьшаем долю сжатия): Линейный расчет с мю 2, расчетное соотношение (устойчивость) - 0,69. Нелинейный расчет с несовершенством - расчет состоялся (1,8 кН - на реальном пределе). Нелинейный расчет с мю 2, расчетное соотношение (устойчивость) - 0,7.
__________________
YouTube Последний раз редактировалось tentovic, 24.02.2023 в 12:40. |
||||||
|
|
|
||||
|
Инженер-философ Регистрация: 24.04.2019
Хабаровск
Сообщений: 2,083
|
Формулы в современном СП списаны с Еврокода. В старом СНиПе были свои.
Формулы в СП (они же в Еврокоде) - это точное аналитическое решение задач устойчивости и геомнелина. При правильном вводе данных в программе ручной счет совпадает с машинным с точностью 3-4 знака. Если не совпадает - значит, в машинном счете накосячено. Расчет на устойчивость не вычисляет несовершенство. Формы потери устойчивости (они же собственные вектора) имеют неопределенную величину, и программы масштабируют их до условной единицы (Старк - тот вообще выводит как попало, не заморачиваясь с нормированием). Величина в миллиметрах определяется нормами, хотя они про это явно не пишут. В случае с СП - множителем в скобках формулы (9) сп 16.2017. Если вводить данные как попало, ответы тоже будут какие попало. Цитата:
Устойивость вычисляется для идеально прямого стержня. А все несовершенства только ухудшают расчет. Если он улучшился - значит, в расчетах накосячено. Цитата:
А где третий пункт - где обычный линейный расчет с мю, который дает правильный ответ по нормам? Даже не догадываюсь. Я не предлагал так считать. Расчет на устойчивость показывает предельную нагрузку, выше которой конструкция не несет при любой прочности материала. А несовершенства определяют, насколько реальная прочность ниже предельной. В этом весь смысл расчета. Неважно, как он сделан - по формулам СП или нелином третьего сорта со знаком качества. Учтены оба фактора - расчет правильный; не учтены - неправильный. Правильный машинный счет сходится с нормативным. Если не сходится - в расчете накосячено. Цитата:
Отсутствие проекта не мешает строить, так же, как отсутствие норм не мешает проектировать  . . |
|||
|
|
|
||||
|
REконструктор истины Регистрация: 23.02.2006
M...nsk
Сообщений: 184
|
Так, заметил свой зевок - в нелинейном расчете с несовершенствами считалось по СН, а не по загружению. В Сочетании силы умножались на коэффициент 1,35 (проскочило автопилотом), а загружение "Несовершенство" на 1. Исправил везде на 1.
Считаем тот же стержень, но только с продольным усилием 54 кН: Линейный расчет с мю 2, расчетное соотношение (устойчивость) - 1,07. Нелинейный расчет с несовершенством - расчет состоялся (54 кН - на реальном пределе). Нелинейный расчет с мю 2, расчетное соотношение (устойчивость) - 1,07. Считаем тот же стержень, но выставляем вертикальную силу 51 кН и добавляем горизонтальную 0,1 кН. Линейный расчет с мю 2, расчетное соотношение (устойчивость) - 1,05. Нелинейный расчет с несовершенством - расчет состоялся (51 кН - на реальном пределе). Нелинейный расчет с мю 2, расчетное соотношение (устойчивость) - 1,23. Считаем тот же стержень, но с продольным усилием 1 кН и поперечным - 2,5 кН (уменьшаем долю сжатия): Линейный расчет с мю 2, расчетное соотношение (устойчивость) - 0,96. Нелинейный расчет с несовершенством - расчет состоялся (2,5 кН - на реальном пределе). Нелинейный расчет с мю 2, расчетное соотношение (устойчивость) - 0,98. На эмпирическом выводе об аутсайдерстве нелинейного расчета с несовершенством ставим жирный крест. Он у нас в лидеры выбился  Впрочем, все значения ложатся очень близко. Кроме варианта, где изгиб едва обозначен. В этом случае "излишний запас по устойчивости" у нелинейго с мю достигает пика. Впрочем, все значения ложатся очень близко. Кроме варианта, где изгиб едва обозначен. В этом случае "излишний запас по устойчивости" у нелинейго с мю достигает пика.----- добавлено через ~8 мин. ----- Цитата:
В СП устойчивость считается по Эйлеру или тоже есть 4 класса сечений и пять кривых потери устойчивости? Даже в моем простейшем примере с квадратной трубой на сжатие, где можно ожидать точного совпадения, есть разница во втором знаке  , по Эйлеру критическая сила - 63,84 кН, по еврокоду - 63,81. А в двутавре каком-нибудь и поболее вылезет. , по Эйлеру критическая сила - 63,84 кН, по еврокоду - 63,81. А в двутавре каком-нибудь и поболее вылезет.Цитата:
 (см. выше). Насчет точности в 3-4 знака - думаю ошибаетесь. Хотя, если строго по одним и тем же формулам простенький стерженек... (см. выше). Насчет точности в 3-4 знака - думаю ошибаетесь. Хотя, если строго по одним и тем же формулам простенький стерженек...Цитата:
*** Кстати, никак не могу осилить границу применяемости линейного из еврокода:  Вроде 1 должна быть. Думал, у белорусов и казахов - очередная ошибка при перепечатывании. Они друг у друга почти все ляпы и ошибки копируют. Поднял аглицкий - тоже 10! А ведь агличане ружей кирпичом не чистют! Что, реально 0,1 от критической - предел?
__________________
YouTube Последний раз редактировалось tentovic, 24.02.2023 в 17:04. |
|||
|
|
|
||||
|
Инженер-философ Регистрация: 24.04.2019
Хабаровск
Сообщений: 2,083
|
Цитата:
Образцы расчетов с трехзначной точностью - в теме: К какой группе предельных состояний относится проверка гибкости? , пост 356 и другие. Вывод формулы из СП - во вложениии в теме Методы определения расчетных длин пригодных для расчетов на устойчивость по СП 16.13330. Ищем, делимся, обсуждаем, пост 339. В тех же темах в других постах - примеры того, как микроны ответ портят. Или чем парабола от синусоиды отличается. Расчеты в Скаде, Старке, Ёкселе и самодельных программах. Да даже в железобетоне они совпадают: Как правильно пользоваться пунктом 8.1.17 СП63.13330 . P.S. Не вижу смысла тратить время дальше на копипасту сюда из старых тем. Появлюсь только если всплывет что-то, что раньше не мелькало. |
|||
|
|
|
||||
|
REконструктор истины Регистрация: 23.02.2006
M...nsk
Сообщений: 184
|
Цитата:
В эмпирической возне в RFEM с "неправильным нелинейным с мю" пока добрался до 23% излишка по расч. соотношению на усточивость. Нюхом чую  максимум (чем антирискую) где-то рядом! максимум (чем антирискую) где-то рядом!Ну и вот, могу улететь до 23% в плюс по устойчивости в очень редких случаях (так пока подозреваю), а на расходе металла - и того меньше. В посте 356 речь идет о " по напряжениям в 1.23 раза", т.е., через площадь сечения напрямую, речь о неменьших издержках только на применении разных стандартов. Повод это ставить крест на "неправильным нелинейном с мю"? Хотя - не угадал. Прогнал разные вариации нагрузок, на этом примере можно улететь в плюс по устойчивости до 42%. Это много. *** И вот еще что. Два правильных метода: линейный и нелинейный с несовершенством, вертикальная сила - 36,4 кН, горизонтальная - 0,8 кН: 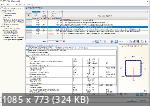  Из всех расчетных параметров похожи друг на друга только "сжатие" и ~"устойчивость -изгиб и сжатие". То есть остальная математика на соответствие результатов по разным методам не претендует вовсе? - Формулы-то одни и те же. В заблуждение вводят! Что с пределом применяемости у линейного - реально 0,1 от критической силы по Эйлеру? - Похоже так и есть. Линейный в этом примере у нас считает за границей применения. *** В общем, на сегодняшний вечер, есть желание уйти от нелинейного с мю на САМЫЙ ПРАВИЛЬНЫЙ В МИРЕ нелинейный с несовершенствами. Но это дело DLUBAL, конечно, недоработал. Должно быть по нажатию ОДНОЙ кнопки. Не API же теперь всякие изучать? *** И еще. Как правильно назначать несовершенства на модели с большим количеством стержней и СН? 1. Есть загружения (вес, снег, ветер), есть сочетания нагрузок из этих загружений (СН). 2. Несовершенства можно создать и из загружений и из СН. 3. В правилах комбинирования можно добраться до зависимостей со специфическими загружениями.  Каков грамотный алгоритм создания/сочетания несовершенств?
__________________
YouTube Последний раз редактировалось tentovic, 24.02.2023 в 22:24. |
|||
|
|
|
||||
|
Цитата:
----- добавлено через ~2 мин. ----- Это нерешаемо, поэтому и не сделано. Общего правила для мю нет. |
||||
|
|
|
||||
|
REконструктор истины Регистрация: 23.02.2006
M...nsk
Сообщений: 184
|
Цитата:
Верю, что сложно. Не уверен насчет "практически невозможно". Если выставить в настройках IMP создание несовершенства по загружениям или СН из RFEM, он может "набить" несовершенство на каждый (почти, зависит от положения и деформации под загружением, видимо) стержень по неким общим правилам (еврокод, пользовательские, пр.). Насколько правильно это сделано - судить не берусь, тема для меня абсолютно новая. Корректировать каждый из сотен или тысяч стержней безумие, конечно. Пока в моей голове все это не утрслось и представления крайне сумбурные. К примеру, есть рама-ферма, как в ней будут приложены несовершенства? По идее, если в плоскости фермы - к отдельным стержням, из плоскости - к блоку стержней целиком. В общем, Ваш приговор - не реально? Здесь я не мю имел в виду, а создание несовершенств. В любом случае - просто ирония  Все новое и сложное пугает. Хочется кнопку! Все новое и сложное пугает. Хочется кнопку!  "Узнай, где у него кнопка, Ури!"  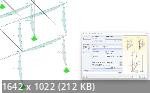 Итак, на своих простеньких туторовских примерах, разработчик показывает, как запросто можно создать несовершенство нажатием если не одной, то 2-3 кнопок. Непонятна бедность настроек, по сути имеем доступ только к описанию загружения и паре формальных опций. Нельзя даже выбрать стандарт. По шелчку открывается диалоговое окно несовершенства конкретного стержня и тут уже можно выбрать стандарт и настроить параметры. Т.е. де-факто предполагается, что автоматом для всего сразу в сложной модели можно создать "рыбу", которую потом править и править. Пока два вопроса: 1. На моделях чуть посложнее, к примеру - безраскосная ферма, два пояса и стойки с каким-то шагом ("лестница" с опиранием по концам рамы), если деформация вдруг из плоскости, то она должна быть создана не для каждого коротенького стерженька, а для пояса целмком? Тогда надо заранее создать блок для каждого пояса и дополнительно к выбору всех стержней добавить еще и этот блок? Если несовершенство будет создано для блока в плоскости рамы - удалить вручную? 2. Насколько правильным будет такой подход? - жестко привязать несовершенства к соответствующим загружениям; несовершенство от снега входит в СН только при наличии в нем снега и т.д.; - правилами комбинирования добавится соответствующее несовершенство главному загружению (в СН возможно только одно несовершенство), если главного загружения нет - будет создано два СН с несовершенством к соответствующему загружению поочередно. Или грамотно (точнее/трудоемче) - только отдельное несовершенство каждому СН (сочетанию нагрузок), рассчитанное конкретно для него? *** Прогнал пространственную модель "тяжелого" арочника под полную снеговую с нелинейным методом по двум вариантам. Первый - с правильными (для линейного метода) мю. Второй - безо всяких мю, но и без несовершенств. На первом ожидал увидеть расчетные соотношения больше предполагаемых "правильных", на втором - меньше. Разница по отдельным стержням, конечно, есть. Но если смотреть сводную таблицу по сечениям (проверка на устойчивость не отключалась) - ничего критического. Все расчетные соотношения уложились между 0,7 и 0,99 и там и там. Как это чудо сработало - ХЗ. Освою несовершенства и будет время - сравню с правильным нелинейным. *** https://rflira.ru/files/events/2021/..._Imperfect.pdf На стр. 6 специалист из "Лиры" интерпретировал английский текст в том смысле, что коэффициенты расчетной длины следует принимать равными единице. "Длина продольного изгиба равна длине системы". "...global imperfections (see 5.3.2) when relevant and may be based on a buckling length equal to the system length". Думаю, он ошибся. Считаем тот же стержень, но с продольным усилием 5 кН и поперечным - 2 кН: Линейный расчет с мю 2, расчетное соотношение (устойчивость) - 0,61. Нелинейный расчет с мю 1, расчетное соотношение (устойчивость) - 0,55. Нелинейный расчет с мю 2, расчетное соотношение (устойчивость) - 0,64. Коэффициент расчетной длины в RF-STABILITY (Расчет собственных чисел) - 1,98. Критическая нагрузка - 63,6 кН. Коэффициент расчетной длины в RF-STABILITY (Нелинейный расчет) - 8,3. Критическая нагрузка - 3,6 кН. Пробуем подобраться к потере устойчивости. Линейный метод тут уже не применим. Считаем тот же стержень, но с продольным усилием 13,6 кН (предел для нелинейного решения) и поперечным - 2 кН: Нелинейный расчет с мю 1, расчетное соотношение (устойчивость) - 0,75. Нелинейный расчет с мю 2, расчетное соотношение (устойчивость) - 1,01. Коэффициент расчетной длины в RF-STABILITY (Нелинейный расчет) - 4,316. Критическая нагрузка - 13,388 кН. Коэффициент критической нагрузки - 0,98. Прогнал тот же стержень с несовершенствами, с продольным усилием 12 кН (предел для нелинейного решения) и поперечным - 2 кН: Коэффициент расчетной длины в RF-STABILITY (Нелинейный расчет) - 4,848. Критическая нагрузка - 10,611 кН. Коэффициент критической нагрузки - 1. На коэф. расчетной длины в RF-STABILITY с нелинейным расчетом нет смысла обращать внимание - они рассчитаны следуя формальной процедуре и, похоже, совсем ни о чём. В RF-STABILITY новый случай пересчитан по сочетанию с несовершенствами. Теперь считаем в RF-STEEL EC3 без несовершенств, они учтены в самих формулах. Нелинейный расчет с мю 1, расчетное соотношение (устойчивость) - 0,7. Нелинейный расчет с мю 2, расчетное соотношение (устойчивость) - 0,93. Даже если логику не включать, на простейшем примере все видно. Нельзя ставить мю=1.
__________________
YouTube Последний раз редактировалось tentovic, 08.03.2023 в 08:45. |
|||
|
|
 |
|
|
 Похожие темы
Похожие темы
|
||||
| Тема | Автор | Раздел | Ответов | Последнее сообщение |
| Подбор коэффициентов расчетных длин элементов | ЮлияStar | SCAD | 3 | 04.05.2017 18:31 |
| Алгоритм определения расчетных длин по Эйлеру в Роботе. | student1991 | Robot | 7 | 29.10.2012 15:37 |
| Расчет ангара в Scad. Вопрос по коэффициентам расчетных длин для связей. | TOWER | SCAD | 9 | 15.07.2009 07:46 |
| Коэффициенты расчетных длин в постпроцессоре SCAD | Pilot729 | SCAD | 4 | 25.12.2006 12:36 |